1. Introduction
Arcadia (1993) de Tom Stoppard s’ouvre sur un échange improbable entre une jeune fille de treize ans (Thomasina) et son tuteur (Septimus) dans lequel le spectateur/lecteur découvre un dialogue qui tresse deux fils apparemment irréconciliables, d’une part le théorème de Fermat1 et, d’autre part, une discussion sur la définition d’une étreinte charnelle :
Thomasina : Is carnal embrace kissing.
Septimus: Yes.
Thomasina : And throwing one’s arms around Mrs Chater ?
Septimus: Yes, now, Fermat’s last theorem—
Thomasina: I thought as much. I hope you are ashamed.
Septimus: I, my lady?
Thomasina: If you do not teach me the true meaning of things, who will?
Septimus : Ah. Yes, I am ashamed. Carnal embrace is sexual congress, which is the insertion of the male genital organ into the female genital organ for purposes of procreation and pleasure. Fermat’s last theorem, by contrast, asserts that when x, y and z are whole numbers each raised to the power of n, the sum of the first two can never equal the third when n is greater than 2.
(Arcadia, Act one, scene one, 3)2
C’est depuis ce rapprochement inattendu, qui est aussi et surtout un écart, que je voudrais situer cette analyse.
L’impression première est celle d’un grand-écart entre notions juxtaposées, d’une disjonction fondamentale et irréconciliable. « Fermat’s last theorem, by contrast », le contraste ne pourrait être plus saisissant entre les deux « définitions » que Septimus convoque. Ressort comique évident, l’association permet aussi dans la diégèse de détourner la conversation et d’éluder la question de la relation avec Mrs Chater. Mais plus fondamentalement encore, la disjonction permet de comprendre ce qui est en jeu lorsque la fiction s’empare de la science. Au niveau énonciatif, comme nous le rappelle très justement Frédérique Aït-Touati, les « enchainements lâches dans les textes de fiction, où l’on saute d’un niveau énonciatif à un autre sans exigence d’un retour au plan de l’énonciation première » s’opposent aux enchaînements « tenus et disciplinés » du raisonnement scientifique. (Aït-Touati 2011: 168). Le mouvement narratif du récit contrarie la dynamique de la démonstration scientifique. Faut-il alors opposer, avec Septimus dans la dernière scène, science et mise en récit : « This is not science. This is storytelling. » (Arcadia : 93)3?
La formulation de Septimus sépare « storytelling » et « science », les consigne dans deux phrases adjacentes et disjointes. À première vue, il serait tentant de voir dans le point qui sépare les deux phrases le signe d’une rupture radicale. Mais d’emblée le tableau se complique. Dans Arcadia, la science est objet de discours ; il y est question de fractales, du second principe de la thermodynamique, ou encore d’algorithmes récursifs. Et le personnage qui confronte fiction et science n’est autre que l’un des deux personnages qui brasse sur scène objets mathématiques et théories physiques. Science mise en scène certes, mais pas uniquement dans le but de « faire vrai ». L’énoncé du théorème de Fermat, dans l’exemple cité plus haut, va au-delà du souci de vraisemblance et de la caution scientifique. Si l’équation est mise en mots, son énoncé n’en demeure pas moins scientifiquement exact. Doit-on alors parler d’intertexte scientifique, au même titre que les références à Anthony and Cleopatra produisent un intertexte shakespearien ?
Poussons un peu plus loin. La remarque de Septimus concerne l’intuition de Thomasina, qui découvre le second principe de la thermodynamique4 avant l’heure. Ce qui est fictif pour le personnage est donc, ironiquement, une découverte scientifique majeure.
L’enchaînement des répliques apporte un ultime méandre. Thomasina rétorque par une question, demandant s’il s’agit d’une valse. Dans la diégèse, Thomasina se réfère à la musique qu’elle entend, mais l’enchaînement que Stoppard nous donne à entendre est le suivant :
Septimus : This is not science. This is story-telling.
Thomasina: Is it a waltz now ? (Arcadia : 93)5
C’est cette valse du discours scientifique et de la fiction que je me propose d’interroger ici.
En employant une métaphore artistique, je me place donc résolument du côté de l’art pour examiner la science, et interroger les oscillations, les hésitations et la circulation des discours. La valse se construit dans la disjonction et à partir de l’écart. Ce qui m’intéresse c’est la mise en fiction dans sa double composante d’écart et de valse. Lorsque la fiction prend la science comme objet, donne-t-elle une représentation adéquate et mobilisable « de la langue, du discours et de la culture »6 des communautés scientifiques ? Que se passe-t-il quand les mathématiques et les équations sont mises en mots et en images ? Comment réconcilier l’écart et le raisonnement scientifique ?
Cette analyse se situe dans la continuité d’une étude que j’ai menée sur la scénographie des mathématiques à l’écran (Le Cor 2010). Mais là où cette première étude s’attachait à la culture mathématique, à son cheminement de pensée et à son esthétique, je m’intéresse ici à l’hybridité discursive propre à la fiction, ainsi qu’à la « confluence de multiples discours » qui caractérise la fiction à substrat professionnel (Isani 2010 [En ligne]). Les chevauchements discursifs permettent de repenser les modalités d’accès au « spécialisé du discours »7 (Petit 2010 [En ligne]) et d’interroger le spécialisé depuis ses limites. Les questionnements soulevés par les croisements entre littérature, fiction et science proposent un éclairage qui n’est ni une analyse de ses caractéristiques linguistiques, ni une étude terminologique, mais qui interroge le spécialisé de la science par sa mise en fiction.
Enfin, en m’attachant au théâtre, aux films et séries télévisées, je souhaite aussi analyser l’aspect multimodal de la science. La physique et les mathématiques se construisent dans un va-et-vient entre plusieurs modes de représentation, dont des objets visuels au titre desquels on peut citer les courbes, les schémas, les dessins géométriques, la modélisation, ou encore des structures plus conceptuelles telles que les matrices, ou même les équations. Le générique de la série Numb3rs est symptomatique en ce sens : le substrat mathématique y est immédiatement identifié par les équations. [Fig. 1]
Figure 1 : Capture d’écran du générique de Numb3rs.
Il s’agira donc d’interroger la composante visuelle de la science et du récit visuel fictionnel, de s’attacher à la mise en espace des composantes non-discursives des mathématiques, d’envisager, donc, leur graphie comme scénographie.
Sans prétendre à une exhaustivité qui dépasserait largement le cadre de mon propos, je m’appuierai sur trois objets issus de genres distincts (théâtre, série télévisée, film), mais comportant tous une composante visuelle et spatiale : Arcadia de Tom Stoppard, la série Numb3rs et le film des frères Wachowski, The Matrix. Ce choix permet d’aller au-delà des caractéristiques propres aux genres particuliers, pour examiner la manière dont l’écriture fictionnelle tresse les mathématiques dans leur composante multimodale.
2. La science mise en mots
Dans Écrire la science, le physicien Etienne Klein s’attache à la « puissance synthétique » des mathématiques, et souligne l’« efficacité stupéfiante » avec laquelle « les mathématiques sont capables de condenser en une simple équation beaucoup de phénomènes physiques différents. » (Ameisen, Klein, Leglu 2010 : 19). Revenons à notre exemple initial. Que se passe-t-il lorsque Septimus met en mots l’équation du théorème de Fermat. En passant de l’équation aux mots, la mise en récit opère un déplacement. Or, « mise en phrases, n’importe quelle équation perd toute concision et l’essentiel de sa puissance, sans rien gagner en intelligibilité pour le profane » (Amseisen, Klein, Leglu 2010: 20). Le mathématicien René Thom présente une opposition plus radicale encore entre les équations et le langage naturel, entre ce qui relève du linguistique et ce qui relève du langage mathématique.
C’est une opposition assez nette. On peut objecter à cela que le langage mathématique exige lui aussi l’utilisation du langage naturel, mais il est certain que, dans le langage mathématique, il y a quelque chose de spécifique qui l’oppose au langage naturel. Je crois que ce qu’il y a de spécifique c’est cette possibilité de définir des variations continues, non descriptibles linguistiquement. Précédemment, nous parlions d’un oscillateur linéaire qui oscille autour d’un point et j’en ai donné une description linguistique. Mais si j’introduis l’espace des phases (p, q) et si je considère les relations H (p,q) = E avec E constant, j’ai immédiatement une description infiniment plus précise que celle purement linguistique. (Thom 1980 : 120)
Réécrire la science pour la mettre en mots reviendrait alors non seulement à l’appauvrir, mais aussi à perdre en précision et donc à dénaturer le langage mathématique.
Vu sous cet angle, le débat de la mise en fiction recoupe celui de la vulgarisation. « Le but de la vulgarisation, », nous dit Klein, « c’est justement de tout dire avec des mots » (Klein 1997 : 18). Le terme vulgariser (popularize) a le plus souvent une connotation négative et « sous-entend qu’il faut dégrader le savoir pour le rendre accessible » (Klein 1997: 16). En mettant en mots, s’agit-il encore du discours scientifique ou n’est-ce plus alors qu’un langage prêté à la science ?
Une précaution s’impose toutefois avant de poursuivre un rapprochement qui pourrait sembler trop hâtif. La vulgarisation vise la transmission des connaissances, la fiction, quant à elle, jouit d’une plus grande liberté. Elle ne prétend rien démontrer et peut tout inventer. Elle n’a pas, non plus, en soi de fonction didactique, même si une des règles du genre semble être des scènes explicatives basées sur des dialogues entre un personnage d’« expert » (mathématicien ou physicien) et un personnage non-scientifique. A titre d’exemple on peut citer la scène où Valentine explique les algorithmes récursifs à Hannah dans Arcadia ou encore la structure des épisodes de Numb3rs, fondée sur les explications que Charlie Epps, le mathématicien, donne à son frère, Don Epps, l’agent du FBI. L’échange s’articule autour d’un jeu de questions/réponses qui permet au spectateur/téléspectateur non-spécialiste de découvrir, avec Don, les théories mathématiques qu’expose Charlie et donc, de pouvoir suivre l’intrigue. Si la finalité diffère, transmission des connaissances d’un côté et déroulement de l’intrigue de l’autre, vulgarisation et mise en fiction proposent toutefois dans les deux cas de mettre en mots les théories, équations et concepts scientifiques. Vulgariser, nous dit Etienne Klein, « c’est finalement raconter des histoires » (Klein 1997: 16). Dans le même ouvrage qui s’attache aux pièges de la vulgarisation scientifique, Paul Caro s’interroge : « La vulgarisation scientifique est-elle plutôt un genre littéraire ? » (Caro 1997 : 3). En partant de ce postulat, le débat sur la vulgarisation scientifique permet donc d’éclairer notre propos.
L’analyse d’Etienne Klein est particulièrement édifiante :
Pour rendre la science accessible aux non-scientifiques, pour la traduire en mots compréhensibles, il faudrait donc effectuer un saut. Rien à voir avec le saut à la perche où le sauteur, sauf accident, est le même à l’arrivée qu’avant. Le saut dont il s’agit ne peut être un simple déplacement : ce doit être une transformation. Il ne s’agit donc pas de transporter la physique telle qu’elle est dans le langage tel qu’il est, de dire ses équations avec des mots ordinaires, mais de la transposer, de la donner à voir et à sentir. (Ameisen, Klein, Leglu : 21)
Ce saut d’un type de discours à un autre, est aussi celui de toute mise en fiction de la science. Les fictions mathématiques8 serait-elles au final une forme de vulgarisation fictionnelle qui estomperait le spécialisé du discours ?
3. Écarts et transposition
Dans son introduction à l’ouvrage d’Olivier Caïra, Jean-Marie Shaeffer aborde la distinction entre connaissance et fiction par la question de la vérité : « La fiction se distingue de la connaissance factuelle non pas parce qu’elle est fausse là où l’autre est vraie, mais parce qu’elle met entre parenthèses la question du vrai et du faux en tant que telle. » (Caïra 2011 : 12). Science et fiction ne sont-elles pas alors deux notions qui s’excluent mutuellement ? Si l’on considère avec le philosophe Jean-Luc Nancy que « le distinct […] c’est toujours l’hétérogène, c'est-à-dire le déchaîné — l’inenchaînable »» (Nancy 2003 : 15), c’est la possibilité même de tisser une science exacte dans la fiction qui est remise en question.
Pour autant, le mélange est-il aussi irréconciliablement hétérogène ? Dans un entretien avec Katherine Kelly et William Demastes, Tom Stoppard revient sur la composition d’Arcadia et explique que la structure même de la pièce prend appui sur les algorithmes récursifs et la théorie du chaos telle qu’elle a été vulgarisée dans le livre de James Gleik, Chaos: Making a New Science : « the structure of Arcadia mimics the reiteration toward chaos, finally. What I’ve read about in Gleick’s book. The play bifurcates two or three times and then goes to the last section, which is all mixed up. So it’s very chaos structured. »9 (Kelly, Demastes 1994: 5). Plutôt que de s’attacher aux éléments de discours scientifique, Stoppard fait ainsi des algorithmes récursifs un principe structurel et dramatique. Le spécialisé n’est plus discursif, il est structurel. La remarque de Valentine sur les algorithmes récursifs peut aussi se lire comme un commentaire sur Arcadia:
Valentine : […] What she was doing is, every time she works out a value for y, she’s using that as her next value for x. And so on. Like a feedback. She’s feeding the solution back into the equation, and then solving it again. Iteration, you see. (Arcadia, scene 4 : 44)10
Les notions d’itération et de « feedback » reflètent la dynamique dramatique. Chaque scène fonctionne comme un nouvel algorithme, qui vient modifier la perception que le lecteur/spectateur a de l’ensemble. Le discours des personnages s’apparente alors à une nouvelle donnée que le spectateur/lecteur réinjecte à l’infini (feed/back ) dans l’équation, et qui nourrit en retour («Like a feedback »11) la représentation. Dès lors, la remarque de Valentine selon laquelle la manipulation, quelle qu’elle soit, relève des mathématiques, semble s’appliquer à la pièce dans son ensemble : « What is the manipulation? Whatever it is, it can be written down as mathematics. It’s called an algorithm. » (Arcadia, Scene 4 : 45)12.
Dans la même veine, le titre du film The Matrix n’est pas une simple métaphore hollywoodienne. Il fait référence à une structure mathématique, la matrice, utilisée notamment en algèbre linéaire et en informatique. Elle s’apparente visuellement à un tableau formé de colonnes et de lignes, et peut donner lieu à toutes sortes d’opérations mathématiques. La structure matricielle et les opérations qu’elle permet informent le film. Dans un article intitulé, « What’s in a name?: The Matrix as Introduction to Mathematics », Kris H. Green explique que le titre fait d’abord allusion au mode de calcul utilisé en infographie pour représenter un objet à l’écran :
To represent an object on a computer screen (or a movie screen, or on the mind of an enslaved human embedded in The Matrix) we define the coordinates of each point on the object. However, in the case of simulating three-dimensional objects, different viewpoints will result in the object taking on different appearances in terms of shape, lighting, texture and so forth. A matrix provides the necessary tool for determining how the shape of an object varies with different viewpoints. […] This is surely an important function of the computer program in the movie, since it must continually construct a shared reality among many different viewpoints and allow each to perceive the virtual world correctly as they interact within it. (Green : 18-19)13
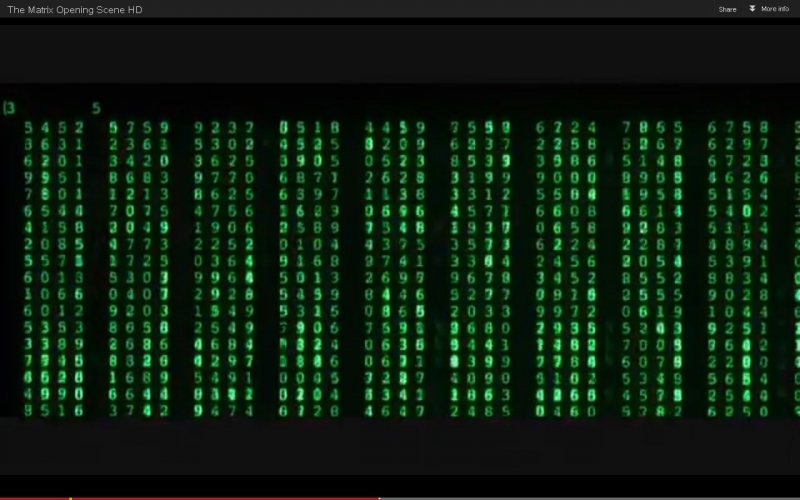
Vu sous cet angle, le générique a une résonance particulière. Les colonnes de quatre chiffres qui défilent sur l’écran [Figure 2] représentent à la fois une matrice de nombres et programme de cryptanalyse, qui tente de décrypter la « réalité », ou plus exactement de décoder la simulation qui tient lieu de réalité dans la diégèse.14
Figure 2 : Générique de The Matrix.
Le titre fait aussi référence d’une part aux processus à l’œuvre dans des chaînes de Markov15 et d’autre part à la théorie des réseaux et la transmission d’information dans un réseau, et donc au mode de fonctionnement des Agents dans le film (Green 19). Dans une chaîne de Markov, les matrices permettent de calculer la probabilité des événements. Pour Green la dernière scène du second volet de la trilogie (The Matrix Reloaded) est l’illustration visuelle de ce calcul de probabilités. (Green : 19).
Figure 3 : The Matrix Reloaded.
La scène oppose Neo (Keanu Reeves) à l’Architecte, et le personnage est entouré d’écrans de télévision qui présentent différentes versions du futur. Au fur et à mesure que Neo reçoit et analyse les informations, toutes les versions convergent vers la même issue. [Fig. 3] Les écrans illustrent donc le mécanisme de calcul et présentent le point d’équilibre vers lequel tendent les suites de variables aléatoires. De même que pour Arcadia, l’ancrage structurel est donc avant tout un ancrage scientifique.
Si la vulgarisation a souvent été envisagée comme une médiation de la science16, la mise en fiction serait plutôt une réécriture en forme de traduction. Il conviendrait alors de s’attacher aux déplacements et reconfigurations qu’une traduction présuppose. Pour Jean-Luc Nancy, « l’écart », « le maintien de la distance » est indissociable de l’art : « C’est là, peut-être que l’art a toujours commencé […] à l’écart.» (Nancy 2003 : 12). Il poursuit son analyse en développant la notion de « distinct ». Le distinct « s’approche à travers la distance, mais ce qu’il apporte au plus près, c’est la distance » (16). L’intérêt de la FASP pour l’anglais de spécialité serait alors à chercher dans ce jeu de convergence et de divergence, d’écart et de rapprochement. D’un point de vue méthodologique, c’est ce jeu avec l’écart qu’il nous faut garder en tête. La mise en fiction maintient la science à distance et permet de s’en approcher tout à la fois.
4. La science en images
Faut-il alors chercher la science hors écran, dans les livres, articles et sites web écrits par les scientifiques et consacrés aux œuvres ? La série Numb3rs a ainsi donné lieu à de nombreuses études qui s’attachent avant tout à démonter les théorèmes hors écran télévisuel, et à détailler les concepts abordés trop rapidement pour être scientifiquement exacts. Les titres des sites web et des articles sont en cela assez explicites : il s’agit avant tout de faire des mathématiques hors écran. A titre d’illustration, on peut noter le titre de l’ouvrage de Keith Devlin et Gary Lorden, The Numbers Behind Numb3rs, ou encore celui du site de Wolfram Research, « The MATH behind NUMB3RS » (http://numb3rs.wolfram.com/). Pour chaque épisode, le site propose un résumé rapide de l’intrigue, suivi d’une rubrique « math used » qui renvoie à une page contenant des définitions et théorèmes. Les épisodes 214 «Harvest » (saison 2) et 113 « Man Hunt » (saison 1) qui traitent des chaînes de Markov sont ainsi reliés à la page suivante :
Figure 4 : Capture d’écran. Weisstein, Eric W. “Markov Chain”.
Le discours mathématique se tient donc en partie hors écran.
Dans l’épisode « Man Hunt », le téléspectateur découvre Charlie devant un tableau noir couvert d’équations :
Figure 5 : « Man Hunt » Numb3rs Episode 13 (Saison 1).
Pourtant, à ce stade, aucune explication n’est fournie. Charlie indique uniquement que les données sont corrompues et que de ce fait, il ne parvient pas à trouver la solution à son problème. Au lieu de s’attacher au spécialisé du discours scientifique, la scène ne retient que la perplexité du personnage. Le tableau couvert d’équations introduit un effet de défamiliarisation qui retranscrit pour le téléspectateur le flottement ressenti par le personnage. Si le terme d’analyse bayésienne (« Bayseian analysis ») est mentionné, il faut aller chercher sa définition hors écran, par exemple sur le site de Wolfram: « Bayesian analysis is a statistical procedure which endeavors to estimate parameters of an underlying distribution based on the observed distribution. »17 (Weisstein). Au final, dans cet exemple, le tâtonnement mathématique est certes traduit dans les images mais uniquement par le biais d’un jeu de déplacement et de transposition.
Pourtant, comme le souligne Luc Pauwels, le discours scientifique est un genre multimédia par excellence. En suivant Lemke, il parle d’hybrides sémiotiques (« semiotic hybrids ») et souligne à quel point les représentations visuelles sont constitutives du raisonnement et du discours scientifiques : « Visual representations are not to be considered mere add-ons or ways to popularize a complex reasoning; they are an essential part of scientific discourse. » (Pauwels 2005 : vii). Dans la même veine, Denis Guedj, mathématicien et auteur de fictions scientifiques, détaille l’importance de la visualisation en science :
La quasi-totalité des scientifiques se donnent un mal fou dans leur laboratoire avec leurs instruments, sur leurs écrans, dans leurs calculs mêmes, pour rendre visible des phénomènes invisibles. 80% de la tâche quotidienne de certains chercheurs consiste à visualiser des phénomènes. (219)
Dès lors, selon Guedj, « Une des tâches de la mise en fiction cinématographique des sciences, c’est la mise en image (la visualisation) des concepts. » (Guedj 1994 : 221). Il cite la manière dont le jeu entre l’image sonore et l’image visuelle permet au cinéma de donner une représentation de l’infini. « Un son qui se perd dans le lointain » permet ainsi de saisir un concept–l’infini, ce qu’une droite finie dessinée sur une feuille elle aussi finie, ne saurait représenter (Guedj 1994 : 221).
En d’autres termes, et pour reprendre la formulation du sociologue Oliver Caïra, ne peut-on pas considérer que la composante visuelle des fictions constituerait une sorte de « documentarité de l’impossible » où l’image remplirait ses objectifs documentaires alors même que la représentation ferait fi de la ressemblance avec des situations envisageables. (Caïra 2011 : 206). Dans son analyse, Oliver Caïra prend l’exemple des planches de dissection des traités d’anatomie du XVIe siècle, « où l’on trouve des gravures qui, du fait de l’impossibilité des situations qu’elles dépeignent, semblent posséder tous les traits de l’image fictionnelle » (Caïra 2011 : 204) mais où la « véracité passe par la justesse du regard » (Hélène Cazes citée par Caïra)18. Il me semble que les séries télévisées telles que Numb3rs offrent une perspective similaire.
Ainsi dans l’épisode « Man Hunt » cité précédemment, une autre scène permet de rendre tangibles les chaînes de Markov, à l’aide d’outils de jardinage et d’un skateboard. Charlie et Larry (le physicien de la série) discutent de l’enchaînement des événements qui a conduit à l’évasion de détenus, après un accident impliquant un bus transportant les détenus et deux autres véhicules. (13 min- 14 :30 min). Pour expliquer son propos, Charlie propose une sorte de reconstitution à l’aide d’un skateboard, d’un semoir (seed spreader) et d’une brouette. Le film de cette reconstitution improbable est interrompu à l’écran par des encadrés qui détaillent les équations auxquelles Charlie fait référence. [Fig. 6]
Figure 6 : « Man Hunt » Numb3rs Episode 13 (Season 1).
Ceci amène les personnages à conclure qu’il s’agit d’une chaîne de Markov et que donc que l’accident a été orchestré : Larry « And that would mean » /Charlie « A Markov Chain.» De manière caractéristique, l’explication complète n’est donnée que dans les deux scènes suivantes et avec l’introduction de personnages non-scientifiques (deux agents du FBI). Ce qui permet à Charlie, d’une part de formuler sa conclusion : « The crash wasn’t an accident, Don, it was staged. »19, et d’autre part de donner une définition des chaînes de Markov :
All these different events and factors, from the initial velocity of the bus to its final torque, all these create what’s called a Markov chain.
What kind of chain?
A Markov chain. A sequence of random values where the probabilities at any given time depend on the values at a previous time.20
Le jeu entre le discours et les images permet non seulement de saisir le concept mathématique mais aussi de capturer le mode de pensée qui permet d’aboutir à une conclusion en probabilité.
5. « Ceci est une fiction »21
Je voudrais conclure par une citation de Tom Stoppard, lors d’une conférence à Caltech, où le dramaturge souligne les points de contact et de divergence entre science et art : «There’s an activity which we call art and an activity which we call science, and to some degree and in certain ways and in different places, they converge; elsewhere they diverge, and elsewhere they interact, and they also intersect.» (Stoppard 1994). Divergence, donc d’abord, parce qu’il s’agit d’une (ré)écriture. Pour reprendre la formulation d’Olivier Caïra, « Ceci est une fiction » et non un document scientifique ou un documentaire. Or, « La fiction ne s’entend pas comme un jeu de contraintes, mais comme la levée des contraintes s’exerçant sur la communication documentaire » (Caïra 2011 : 79). Là où le film scientifique revêt le sceau de l’authenticité, la liberté d’écriture propre à la fiction suppose un « espace ouvert » (Caïra 2011 : 79) ne nécessitant pas d’avoir une source fiable et identifiable. De ce fait, l’ancrage (encrage?) fictionnel introduit une distance qu’il nous faut garder en tête.
Pour autant, le mouvement de va-et-vient entre le récit fictionnel et la science crée une zone de contact, où fiction et science interagissent. Il ne s’agit plus de se demander si la Science est dégradée lorsqu’elle s’écrit, mais plutôt d’envisager ces (ré)-écritures comme une transposition, et de chercher ce qui s’y gagne.
Convergence, donc, parce que paradoxalement, si les équations complexes ne se transcrivent pas, les séries et films mettent en lumière une méthode et une démarche. Au final, les images permettent mieux que n’importe quel discours de visualiser les concepts.